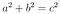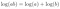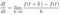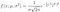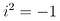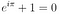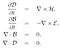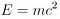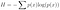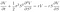A selection of the most important and beautiful mathematical equations
Throughout the ages, mathematics has helped us to better understand the world, and likewise, we used the world to better understand math. The discipline of mathematics is built on human experiences and common ideas developed over thousands of years. Some new mathematical discoveries have changed the world, in the sense that by the use of math, we are able to explain more phenomenons and connections that appear in this world.
In this article, I will show 10 of the most important and beautiful mathematical equations. This article is based on the book “In Pursuit of the Unknown: 17 Equations That Changed the World” by Ian Stewart.
1. Pythagoras’s Theorem (Pythagoras, 530 BC)

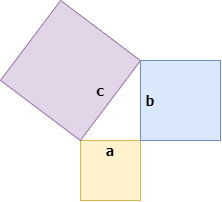
The Pythagorean theorem is the oldest out of the ten listed here, and is almost 2500 years old! This theorem states a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) equals the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the “Pythagorean equation” (stated above), where c represents the length of the hypotenuse and a and b are the lengths of the triangle’s other two sides.
2. Logarithms (John Napier, 1610)

The above equation of the logarithm immediately displays one of its most important applications: it is able to turn multiplication into addition. Years ago, when all calculations had to be done by hand, this property did lead to much faster calculations.
Of course, this is not its only use. As is generally known, the logarithm is an inverse operation, since it is able to undo exponential effects. Furthermore, the logarithm is a very convenient way to express large numbers (the base 10 logarithm of a number is roughly the number of digits in that number: log(98765) ≈ 4.99).
3. Calculus (Newton, 1668)

The above equation is the definition of the derivative in calculus. The derivative measures the rate at which a quantity changes. The derivative has many important applications both from elementary calculus, to multivariate calculus, and far beyond.
4. Normal Distribution (C.F. Gauss, 1810)
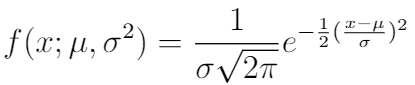

The normal distribution is the most important probability distribution in statistics. This is the case since this distribution fits many natural phenomena. This distribution is also known as the Gaussian distribution, named after C.F. Gauss. As can be seen from the picture, it is a symmetric distribution. The normal distribution depends on two parameters: the mean μ and the standard deviation σ. These two parameters define the shape and probabilities of the normal distribution entirely. The mean defines the location of the peak for the normal distribution, and the standard deviation defines the width. Extreme values in both tails of the distribution are similarly unlikely.
The normal distribution is frequently used in applications such as IQ scores measurement errors and height distributions.
5. Square Root of Minus One (R. Descartes, 17th century)

This equation is the foundation of complex numbers, that can be written as a real number multiplied by the imaginary unit i. Complex numbers are used in real-life applications such as electrical circuits.
6. Euler’s Identity (Euler, 1748)

This equation is considered to be an exemplar of mathematical beauty since it shows a profound connection between the most fundamental numbers in mathematics. A poll of readers, conducted by The Mathematical Intelligencer in 1990, named Euler’s identity as the “most beautiful theorem in mathematics”. In another poll of readers, that was conducted by Physics World in 2004, Euler’s identity tied with Maxwell’s equations as the “greatest equation ever”.
7. Maxwell’s Equations (J.C. Maxwell, 1865)

Maxwell’s equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics and electric circuits. These equations describe how electric and magnetic fields are generated by charges, currents, and changes of the fields.
An important consequence of Maxwell’s equations is that they demonstrate how fluctuating electric and magnetic fields propagate at a constant speed (c) in a vacuum.
8. Relativity (Einstein, 1905)

This classic equation states that anything having mass has an equivalent amount of energy and vice versa (mass-energy equivalence). The equivalent energy (E) can be calculated as the mass (m) multiplied by the speed of light (c) squared. Since the speed of light is a large number in everyday units, the formula implies that even an everyday object at rest with a modest amount of mass has a very large amount of energy intrinsically.
9. Information Theory (C. Shannon, 1949)

The given equation is for information entropy, which is a quantity in information theory associated to any random variable. This entropy is a measure of disorder. Here, it measures the information content of a message (a book, a JPEG picture, or anything that can be represented symbolically). The entropy of a message represents a lower bound on how much that message can be compressed without losing some of its content.
This entropy measure, introduced by Shannon, launched the mathematical study of information, and the results are central to how we communicate over networks today.
10. Black-Scholes Equation (F. Black and M. Scholes, 1990)
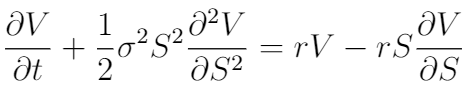
The Black-Scholes equation describes how finance experts and traders find prices for derivatives, which are financial products based on some underlying asset. Derivatives are a major part of the modern financial system.
The above equation is for a European call or put option on an underlying stock that pays no dividends. Here, V is the price of the option as a function of stock price S and time t, r is the risk-free interest rate, and σ is the volatility of the stock.
The key insight behind the equation is that, under the model assumption of a frictionless market, one can perfectly hedge the option by buying and selling the underlying asset in just the right way and consequently “eliminate risk”. This hedge, in turn, implies that there is only one right price for the option, as returned by the Black-Scholes formula.
The left-hand side of the equation consists of a “time decay” term, the change in the derivative value with respect to time, and a term involving the second spatial derivative, the convexity of the derivative value with respect to the underlying value. The right-hand side is the riskless return from a long position in the derivative and a short position.
Conclusion
In this article, we have seen 10 world-changing mathematical equations. Of course, there are many-many more mathematical discoveries that have had a huge impact on the world. Math keeps evolving, and so will our society.