Using Graph Theory to save yourself a fortune on security guards!
Daniel Ochoa
Suppose you are the owner of a famous art gallery in New York containing priceless paintings and sculptures. Given that it’s one of the most widely visited art galleries, there is a chance that a robbery can transpire. You would like security guards to guard the entire gallery at any given time. However, once you check your budget, you realize you are in a tight pinch…
Given the art gallery’s layout, what is the minimum number of stationary guards placed on the corners of the art gallery needed to ensure its security from potential invaders.
History
The Art Gallery Problem was first posed in 1973 by the mathematician Victor Klee. In 1975, Václav Chvátal proved using the method of induction that for simple polygons ⌊n/3⌋ guards is sufficient to guard the gallery when there are n vertices in the polygon. In 1978, Steve Fisk created a more clear proof via triangulation and coloring of vertices.
Terminology
- Vertex: One of the points on which the graph is defined and which may be connected by graph edges
- Edge: a line or arrow extending from one vertex to another.
- Triangulation of a polygon: a decomposition of the polygon into triangles by drawing non-intersecting diagonals between pairs of vertices
- Graph Coloring: an assignment of labels or colors to each vertex of a graph such that no edge connects two identically colored vertices.
- Floor Function ⌊n⌋ : the largest integer less than or equal to n.
How can we approach the solution to this problem?
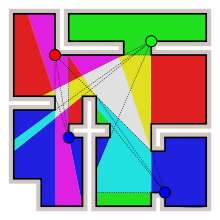
If we assume guards can only be placed at the museum’s corners, then each corner is represented by a vertex.
To solve this problem, we need to show that there are positions in the museum’s floor plan such that a minimum number of 1 guard is required to observe every point in the museum.
There is more than one way to find a solution to this problem. Let’s examine Chvátal’s Art Gallery Theorem & Fisk’s Proof.
Chvátal’s Art Gallery Theorem
Since each guard can see at least two other vertices, or the two vertices adjacent to the guard’s vertex, each guard is responsible for at least three vertices. Thus, the two vertices adjacent to the guard’s vertex do not require additional guards.
We can conclude that the maximum number of guards for a polygon with n vertices is n/3. However, we can’t have a decimal for a guard, so we must use the floor function to round down. Therefore, the maximum number of guards needed is ⌊n/3⌋.
Fisk’s Proof
- First, we must triangulate the polygon.
- Next, we need to 3-color the vertices of the polygon. What that means is we need to assign each vertex one of three colors so that no adjacent vertices have the same color. For this problem, a vertex can be either a red, green, or blue color.
- Then, we pick one of the three colors. Each vertex of that color will represent a guard because each triangle formed from triangulating the polygon has only one vertex of each color.
- Repeat Step 3 for each of the colors. The color with the least number of vertices will be the minimum number of guards required.
Extensions of the Original Problem
Now that we understand the mathematics behind the original problem, it is time to examine if we can create new questions from a question. Unsurprisingly, it turns out that we indeed can!
- What if the art gallery represents itself as an orthogonal polygon? (An orthogonal polygon is a polygon where each edge meets a 90-degree angle):
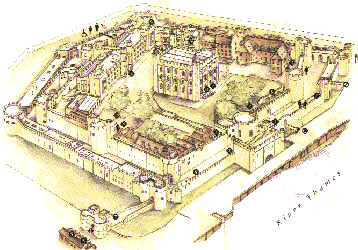
- What if the guards need to guard an outdoor area? What is the minimum number of guards required to see the exterior of a simple polygon?
This area can be illustrated by the fortress below:

3. What if the art gallery is designed as a three-dimensional solid. That means that the art gallery will not have to be guarded with guards placed at the vertices necessarily. Although the surface is entirely secure, there may be points in the interior that are not guarded, even if there is a guard on each vertex.

Real-life Applications
The Art Gallery Problem is a visibility problem in computational geometry, a mathematical field that involves the design, analysis and implementation of efficient algorithms for solving geometric input and output problems.
Computational Geometry can be applied to several fields such as:
- Route planning for GPS; determining location, speed, direction.
- Integrated Circuit Design.
- Computer vision, to determine lights of sights and designing special effects in movies.
- Robotics, to plan mobility and visibility.
- Designing and building objects such as cars, ships, & aircraft.
Conclusion
Now that YOU know the minimum number of guards necessary to guard your art gallery, museum, or building containing valuable items, you will save a fortune amount of money on anti-criminal security.